Stokastik dinamik sistemler, finansal piyasalardaki varlık fiyatları, beyindeki nöral aktivite veya bulaşıcı hastalıkların yayılması gibi birçok bilimsel alanda ortaya çıkar. Petar Jovanovski’nin Doktora Tez, kısmen rastgele olan şekillerde gelişen bu sistemlere odaklanır. Jovanovski, 19 Eylül’de doktora tezini “stokastik dinamik sistemlerin veri koşullu simülasyonuna dayanan simülasyon tabanlı parametre çıkarım yöntemlerini” savunacak.
Bu işlemler diferansiyel denklemler kullanılarak tarif edilir. Dinamiklerdeki rastgelelik klasik bir örneği Brown harekettir: suda asılı, çevredeki moleküllerle çarpışmalarla tahrik edilen polen parçacıklarının düzensiz hareketi. Yörüngenin pürüzsüz ve öngörülebilir olduğu tamamen deterministik sistemlerden farklı olarak, stokastik süreçler rastgele dalgalanmaları altta yatan bir eğilimle birleştirir. Bu tür fenomenleri incelemek için araştırmacılar stokastik diferansiyel denklemler (SDES) kullanırlar.
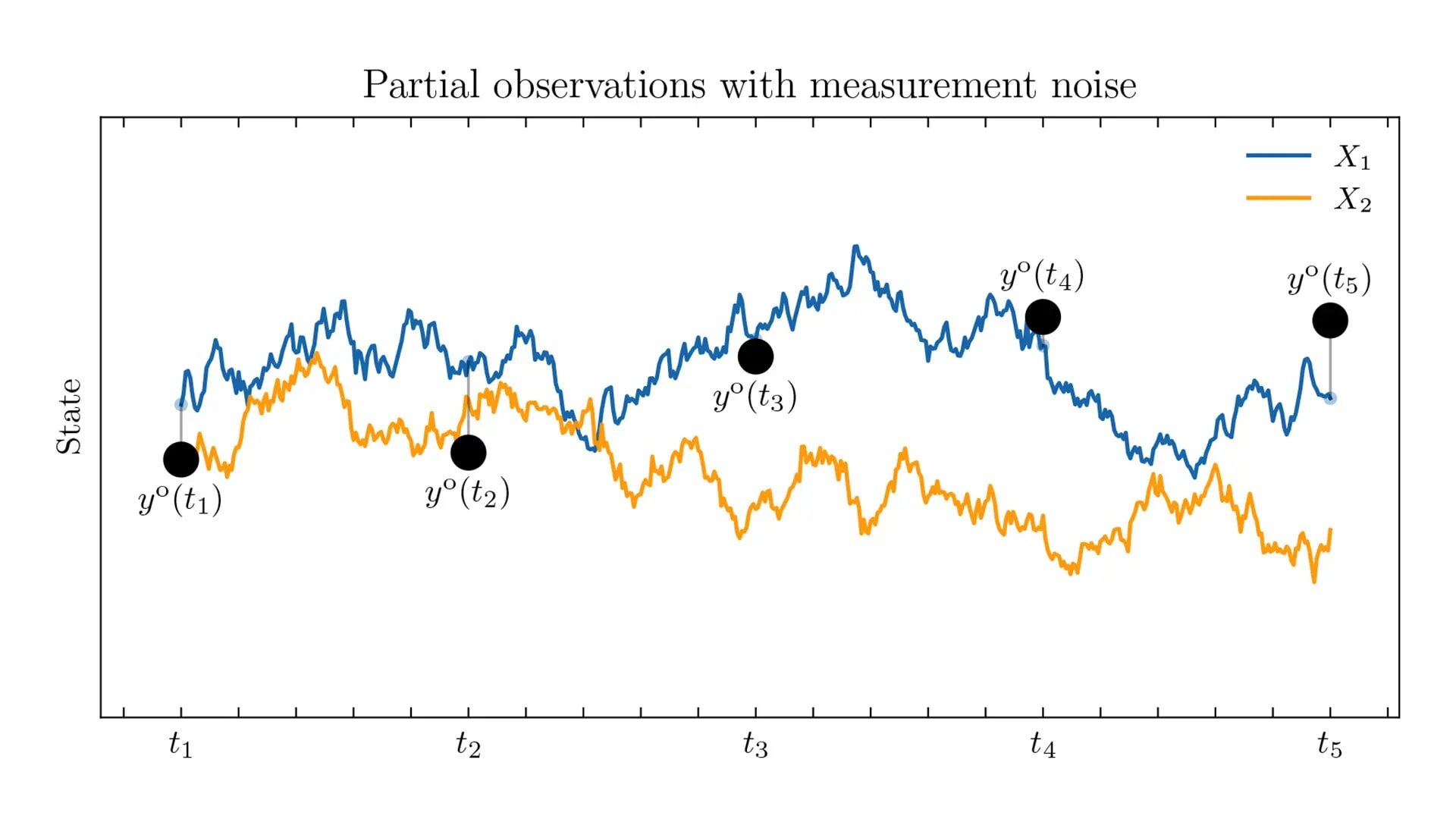
“Tezin çoğu sürekli zaman modellerine odaklanıyor, ancak bir makale ayrı zaman sistemlerini de dikkate alıyor. Davranış zaman içinde sürekli olmasına rağmen, bunu sadece ölçüm gürültüsü ile bozulan ayrı noktalarda gözlemliyoruz.
Jovanovski, “Merkezi amaç parametre çıkarım: Bu modellerin parametrelerinin veriler göz önüne alındığında posterior dağılımlarını hesaplayarak bir Bayesian çerçevesinde tahmin etmek. Ancak, olasılık fonksiyonu analitik olarak inatçı olduğu için, standart istatistiksel araçlar doğrudan uygulanamaz” diyor Jovanovski.
Simülasyonlara rehberlik etmek için gözlemlenen verileri kullanan yöntemler
Yaklaşık Bayesian hesaplaması (ABC), simüle edilmiş verilerin üretilmesine ve daha sonra simülasyonların gözlemlenen verilere ne kadar yakın olduğunu değerlendirmeye dayanan Bayes istatistiklerinin bir dalıdır. SDE bağlamında, fikir parametreleri simüle etmek, bu parametreler altında yörüngeler oluşturmak ve gözlemlenen verilere yeterince yakın simülasyonları korumaktır.
Bazı yörüngeler, parametrelerin zayıf olması nedeniyle rastgele nedeniyle reddedilebilir. Bunu ele almak için, veri koşullu bir çerçeve geliştirilmiştir: tamamen SDE’den yörüngeleri simüle etmek yerine, simülasyonlar doğrudan gözlemlenen verilere koşullandırılmıştır.
Bu yöntemler, örneğin, gürültü kaynaklı bistabilite sergileyen oldukça değişken Schlögl modeline uygulanmıştır ve bu zorlu durumda çıkarım elde edilmiştir. Ek olarak, standart sayısal yöntemlerin yakalanamadığı yapısal özellikleri koruyan kimyasal reaksiyon ağları için yeni bölünme şemaları sunulmuştur. Genel olarak, bu ilerlemeler simülasyon ret oranlarını azaltır ve stokastik dinamik sistemler için daha hızlı, daha güvenilir bir çıkarım sağlar.