Görünüşte öngörülemeyen ve böylece kontrol edilemez, canlı organizmaların dinamikleri uzun zamandır bilim insanlarını şaşırttı ve büyüledi. Bu dinamikler çeşitli biyolojik sistemleri modelleyebilen reaksiyon ağları ile temsil edilebilirken, bu dinamikleri evcilleştirme ve kontrol etmek zor olabilir.
Şimdi, Japonya’dan araştırmacılar, bilgi teorisinden kavramları entegre ederek kontrol problemini çözmek için büyük bir adım attılar.
Yayınlanan bir makalede PRX LIFETokyo Üniversitesi Endüstriyel Bilimler Enstitüsü’nden araştırmacılar, canlı organizmaları içerenler gibi dinamik ağlar için optimizasyon stratejileri tasarlamak için kullanılabilecek matematiksel bir teori geliştirdiler.
Araştırmacılar, bir sistemi mümkün olan en iyi ödüle yönlendirebilecek stratejileri inceleyen bir matematik dalı olan optimal kontrol teorisini kullandılar. Bu teorinin günlük uygulamaları, kendi kendine giden otomobiller, robotlar ve finansal planları içerir. Bununla birlikte, bu teoriyi, ayrı nüfus boyutları, doğrusal olmayan çok fazla etkileşimler ve Gauss dışı rastgele, geleneksel sürekli, doğrusal ve Gauss sistemlerinden çok farklı olan biyolojik sistemlere uygulanması zordur.
“Kontrol teorisi uygulamalarının çoğu sorunsuz bir şekilde değişen şeyleri içerir, ancak biyolojik sistemler genellikle farklı sıçramalar sergiler” diyor. “Ayrıca, biyolojik bir nüfus soyu tükenebilir, bu da bu sistemleri modellerken büyük bir komplikasyon sunar.”
Nüfus dinamikleri son derece doğrusal değildi-değişkenler arasındaki ilişkiler çok büyüktü-optimizasyon problemini çözmek son derece zorlaştırdı. Bununla birlikte, ekip, başka bir matematik dalından, bilgi teorisinden araçların, bunları basitleştirmek için tam olarak ihtiyaç duyduklarını sağladığını buldu.
Özellikle, iki olasılık dağılımının ne kadar benzer olduğunu ölçen F-Digerans, araştırmacılara daha basit bir çözüm bulmanın bir yolunu veren birkaç arzu edilen matematiksel özelliklere sahipti.
Kıdemli yazar Tetsuya J. Kobayashi, “Doğrusal olmayan optimizasyon problemlerini verimli bir şekilde çözmek genellikle zordur.”
“Bununla birlikte, bizim durumumuzda, doğrusal olmayan denklemimizi doğrusal bir denkleme dönüştürmek için, Kullback-Leibler Diverjence ile birlikte Cole-Hopf dönüşümü adı verilen az bilinen bir numara kullanabildik.”
Yeni matematik çerçevesinin gücü, ne kadar geniş bir şekilde uygulanabileceğidir. Diğerlerinin yanı sıra moleküler motor taşıma, biyolojik çeşitlilik ve salgın kontrolü gibi çeşitli konuları araştırmak için kullanılabilir. Geliştirilen modelin, görünüşte zıt ve çeşitli senaryolar için ortak olan belirli davranışları açıkladığı gösterilmiştir.
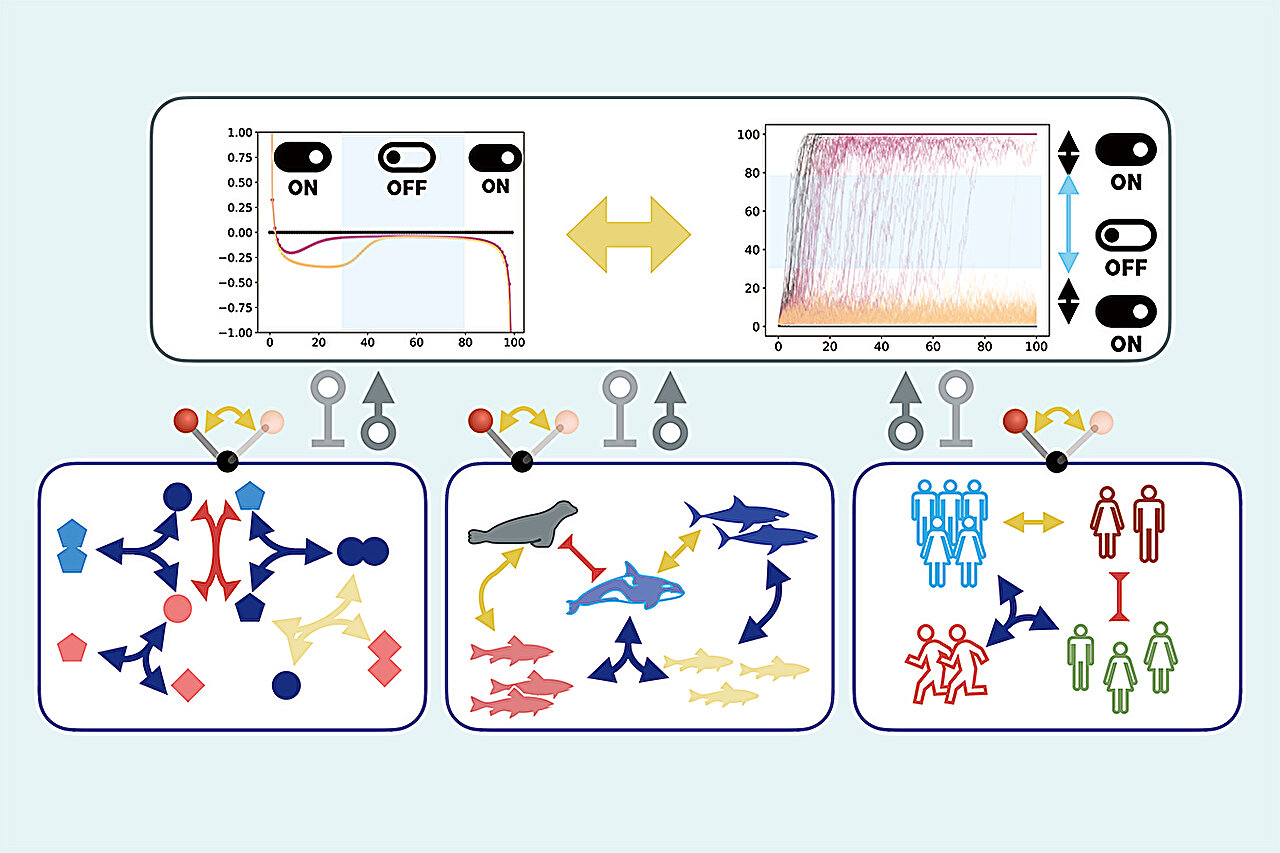
Horiguchi, “Zamanla hızla büyüyebilen veya azalabilecek sistemlerde, optimal stratejinin bir bekleme süresi ile aktif bir dönem arasında geçiş yapabileceğini bulduk.” Diyor.
“Örneğin, tür çeşitliliğinin korunmasında, aktif müdahaleler sadece türlerden biri ciddi bir düşüş yaşadığında ve yok olma ile tehdit edildiğinde etkilidir. Diğer biyolojik sistemler için optimal stratejiler bu mod değiştirme stratejisini paylaşabilir.”
Bu bulguların bir dizi konu için geçerli olabileceği göz önüne alındığında, bu çalışma, tıp, çevre yönetimi ve sentetik biyoloji gibi çeşitli alanlardan fenomenleri açıklama ve geliştirme vaat etmektedir.
Ekip, bu yeni çerçevenin daha büyük ve daha karmaşık biyolojik sistemleri ele almak için genişletilebileceği konusunda iyimser.