Kuantum bilgi işlem dünyasında, Hilbert uzay boyutu – kuantum bilgisayarın erişebileceği kuantum sayısının ölçüsü – ödüllü bir mülktür. Daha büyük bir Hilbert boşluğuna sahip olmak, daha karmaşık kuantum işlemlerine izin verir ve kuantum bilgilerinin gürültü ve hatalardan korunması için gerekli olan kuantum hata düzeltmesinin (QEC) sağlanmasında önemli bir rol oynar.
Yale Üniversitesi’nden araştırmacılar tarafından yapılan yeni bir araştırma Doğa Kuantum bilgisine sahip olan ve ikiden fazla eyalette var olabilecek bir kuantum sistemi olan Qudits yarattı. Bir qutrit (3 seviyeli kuantum sistemi) ve bir ququart (4 seviyeli kuantum sistemi) kullanan araştırmacılar, Gottesman-Kitaev-Preskill (GKP) Bosonic kodunu kullanarak daha yüksek boyutlu kuantum birimleri için ilk deneysel kuantum hata düzeltmesini gösterdiler.
Piyasadaki çoğu kuantum bilgisayar genellikle kupit adı verilen kuantum durumlarını kullanarak işler-Kuantum süperpozisyonu nedeniyle, yukarı (1) ve aşağı (0) ve aynı zamanda hem 0 ve 1’de iyi tanımlanmış iki durumda var olabilen normal bir bilgisayarda biraz benzer birimler. Tek bir kubitin Hilbert boşluğu iki boyutlu bir kompleks vektör boşluğudur.
Daha büyük olduğundan, Hilbert alanı durumunda, kubit yerine qudit kullanımı çok fazla bilimsel ilgi kazanmaktadır.
Qudits, kuantum kapıları inşa etmek, algoritmalar çalıştırmak, özel “sihir” durumları oluşturmak ve karmaşık kuantum sistemlerini her zamankinden daha kolay simüle etmek gibi zorlu görevler yapabilir. Bu güçlerden yararlanmak için, araştırmacılar yıllarca foton, ultraold atomları ve moleküller ve süper iletken devreler yardımıyla Qudit tabanlı kuantum bilgisayarlar inşa ettiler.

Kuantum bilgi işlemin güvenilirliği, kırılgan kuantum bilgilerini gürültü ve kusurlardan koruyan QEC’ye bağlıdır. Yine de, QEC’deki deneysel çabaların çoğu sadece kubitlere odaklanmıştır ve bu nedenle Qudits bir arka koltuk aldı.
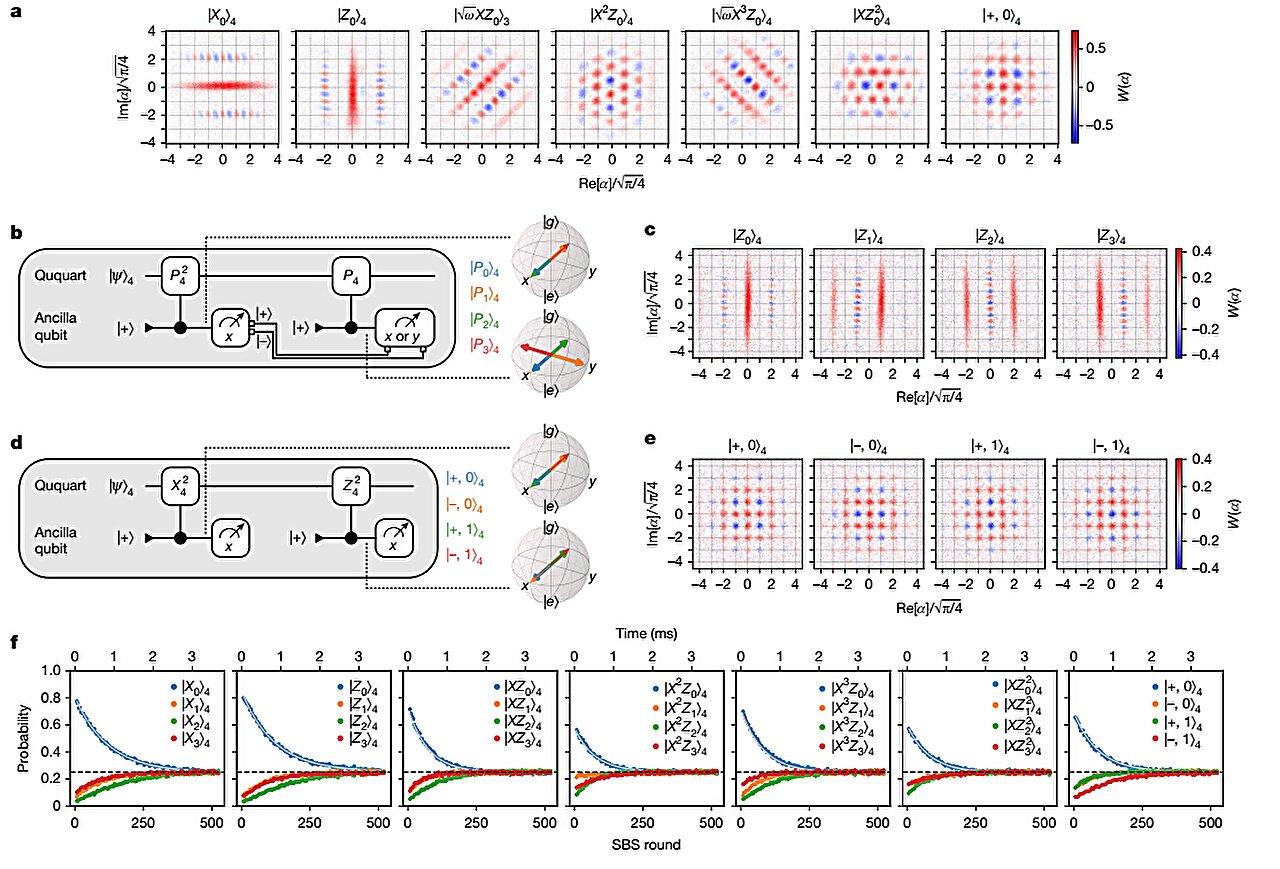
Bu çalışmadaki araştırmacılar, Gottesman -Kitaev – Preskill (GKP) Bosonic kodunu kullanarak bir qutrit ve bir Ququart için ilk deneysel hata düzeltme gösterisini sundular. Sistemleri üçlü ve kuaterner kuantum anıları olarak optimize etmek için, araştırmacılar, hataları düzeltmek veya kuantum kapılarını çalıştırmak için en iyi yol bulmak için bir deneme ve hata yöntemi kullanan bir tür makine öğrenimi türü olan bir takviye öğrenme algoritması seçtiler.
Deney, daha büyük bir Hilbert alanının gücünü kullanarak QEC için daha pratik ve donanım tasarruflu bir yöntem sergileyen hata düzeltmesi için başabaş noktasını geçti.
Araştırmacılar, GKP Qudit durumlarının artan foton kaybı ve defazing oranlarının, mantıksal quditlerde kodlanan kuantum bilgisinin ömründe mütevazı bir azalmaya yol açabileceğini, ancak karşılığında, tek bir fiziksel sistemde daha mantıklı kuantum durumlarına erişim sağladığını belirtiyor.
Bulgular, sağlam ve ölçeklenebilir kuantum bilgisayarları gerçekleştirme vaadini göstermektedir ve kriptografi, malzeme bilimi ve ilaç keşfinde atılımlara yol açabilir.