Araştırmacılar, hataya dayanıklı kuantum hesaplamada kritik bir darboğaz olan sihirli durum damıtma için teorik olarak en uygun ölçeklendirmenin kübitler için elde edilebileceğini ve tam olarak sıfır ölçeklendirme üssüne ulaşarak önceki en iyi sonucun iyileştirilebileceğini gösterdi.
Çalışma, şu tarihte yayımlandı: Doğa Fiziğialanda yıllardır devam eden temel bir açık sorunu çözüyor.
Ph.D. Adam Wills, “Genel olarak kuantum bilgisayarları üretmenin harika ve ilham verici bir hedef olduğunu düşünüyorum” dedi. MIT Teorik Fizik Merkezi öğrencisi ve çalışmanın baş yazarı CEİD’a söyledi.
“Ancak bu son derece zorlayıcı bir hedef. Halihazırda kuantum bilgisayarlara sahip olmamamızın en büyük nedeni gürültü sorunudur. Kübitler son derece kırılgandır ve çevre tarafından yok edilir ve bazı hata düzeltme kodlarıyla korunmaları gerekir.”
Ancak hata düzeltme tek başına yeterli değildir. Kübitleri koruyan kodlar doğal olarak yalnızca Clifford kapıları adı verilen ve tek başına kuantum avantajı sağlayamayan belirli işlemleri destekliyor. Gerekli Clifford dışı operasyonların hataya dayanıklı bir şekilde uygulanması büyük bir darboğaz olarak kaldı.
Bravyi ve Kitaev tarafından 2005 yılında tanıtılan sihirli durum damıtma, bu işlemleri özel olarak hazırlanmış kuantum durumları aracılığıyla mümkün kılarak bu sorunu çözüyor. Bununla birlikte, hata oranları azaldıkça artan ek yük (yüksek kaliteli çıktı durumu başına ihtiyaç duyulan gürültülü giriş durumlarının sayısı) nedeniyle süreç son derece kaynak yoğun olmaya devam etti.
Kuantum hesaplamanın büyüsü
Kuantum hesaplamada sihir, Bravyi ve Kitaev’in çalışmalarından kaynaklanan bir kavram olan, kesin olarak ölçülebilir bir kaynaktır. Çalışmalarına göre, Clifford operasyonları sihirli durumlar adı verilen özel kuantum durumlarıyla desteklendiğinde evrensel kuantum hesaplama mümkün hale geliyor.
Tüm kuantum durumlarını büyük bir küme olarak düşünün. Dengeleyici durumlar klasik bilgisayarların ayak uydurabileceği bölgeyi temsil eder. Sihirli durumlar bu bölgenin dışında yer alır ve ekstra bir kaynak olan kuantum bağlamsallığına sahiptir. Bu, kuantum bilgisayarlara klasik sistemlere göre avantaj sağlıyor.
Bu durumlar, evrensel kuantum hesaplaması için gerekli olan Clifford olmayan kapıları yürütmek için kapı ışınlanması adı verilen bir süreç aracılığıyla tüketilebilir. Örneğin, bir T kapısı, yalnızca Clifford işlemleri ve ölçümleri kullanılarak bir sihirli durumun tüketilmesiyle uygulanabilir.
Bununla birlikte, araştırmacılar yalnızca nispeten yüksek hata oranlarına sahip, genellikle 10 civarında, gürültülü sihirli durumlar üretebilirler.-3Wills’e göre. Kuantum avantajı için hata oranlarının yaklaşık 10’a düşmesi gerekiyor-7ve büyük ölçekli algoritmalar için 10’a kadar düşük oranlar-15 veya daha düşük olması gerekir.
Ekibin optimize etmek için yola çıktığı süreç olan sihirli durum damıtmanın devreye girdiği yer burasıdır.
Sürekli ek yüke ulaşmak
Sihirli durum damıtmanın verimliliği, ek yüküyle ölçülür: giriş sihirli durumlarının, hedef hata oranına ulaşmak için gereken çıktı sihirli durumlarına oranı.
Onlarca yıldır bu ek yük, γ (gamma) adı verilen bir ölçeklendirme üssü ile karakterize edilen hedef hata oranı azaldıkça arttı. γ ne kadar küçük olursa damıtma o kadar verimli olur. γ = 0’a ulaşmak, son durumların ne kadar temiz olması gerektiğine bakılmaksızın sabit ek yük anlamına gelir.
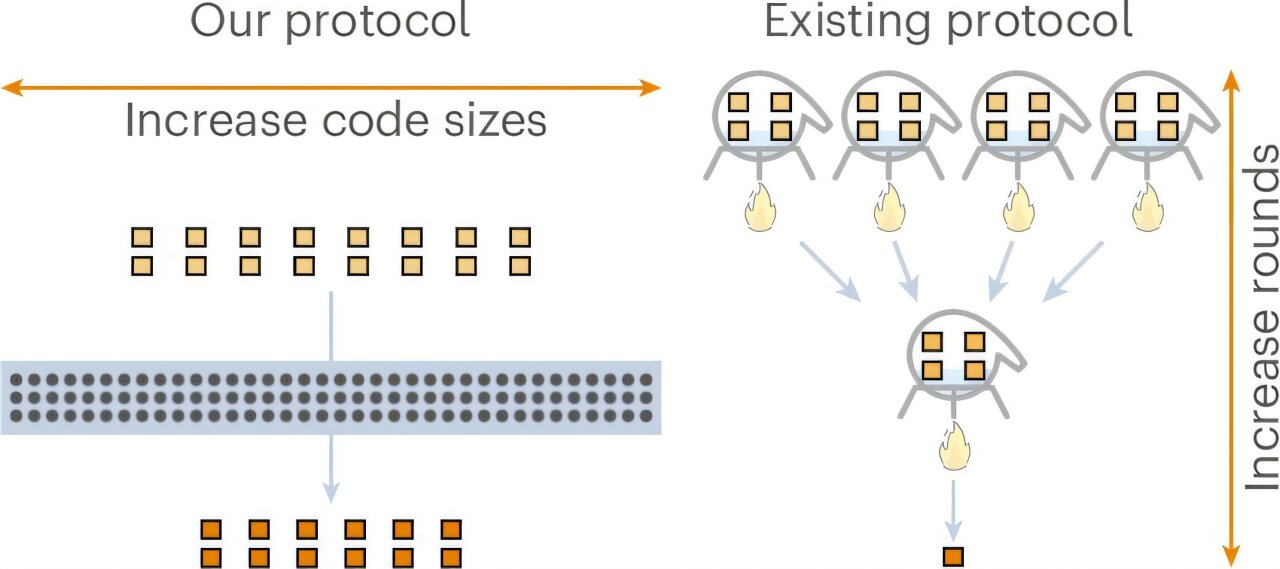
Alan bu ölçeklendirmeyi azaltma konusunda istikrarlı bir ilerleme kaydetti. Hastings ve Haah 2017’de γ ≈ 0,678’e ulaştı. Krishna ve Tillich 2018’de γ → 0’a ulaştı, ancak bu sadece pratik kübit sistemlerine giden net bir yol olmayan, sürekli büyüyen boyuttaki kuantum sistemleri içindi. Wills ve meslektaşları γ = 0’ın mümkün olduğunu kanıtladılar.
Wills, “Sürekli sihirli durum damıtma işleminin mümkün olduğunu gösteriyoruz” dedi. “Bu, yeterince büyük, yeterince doğru ve yeterince uzun bir algoritma çalıştıran bir kuantum bilgisayarınız varsa, yöntemlerimizin sihri damıtmanın en iyi yolu olacağı anlamına geliyor.”
İki aşamalı bir keşif
Wills, “Bu sonucun keşfedilmesi aslında birkaç ay arayla gerçekleşen iki aşamada gerçekleşti” diye açıkladı. “İlk fark, cebirsel geometri kodlarının bu problem için gerçekten yararlı olacağıydı.”
Önceki girişimlerde farklı türde klasik hata düzeltme kodları kullanılmıştı. Hastings ve Haah, Reed-Muller kodlarını kullandılar ancak γ ≈ 0,678’in altına inemediler. Krishna ve Tillich, γ = 0’a yaklaşmak için Reed-Solomon kodlarını kullandılar, ancak onların yaklaşımı, pratik olmayacak kadar büyük boyutlarda kuantum sistemleri gerektiriyordu.
1980’lerden kalma bir kod sınıfı olan cebirsel geometri kodları, sabit boyutlu kuantum sistemleriyle çalışırken güçlü hata düzeltme özelliklerine sahiptir. Bu, pratik kuantum bilgisayarlarda kullanılan iki seviyeli kübitler için değil, 1024 boyutlu kuditler (1.024 seviyeli kuantum sistemleri) için sabit bir yük elde etti.
Wills, “İkinci keşif, Dan Gottesman’ın halen üzerinde çalışılan bir ders kitabını okurken geldi” dedi. “Nispeten belirsiz bir bölümden geçerek, kubitlerimizi kubit kümeleri olarak gerçekleştirebileceğimizi gördük.”
1024 boyutlu bir kudit (210 boyutlar) matematiksel olarak 10 kübit (2 × 2 × 2… on kez) olarak temsil edilebilir. Bu, ekibin sabit yük protokollerini kuditlerden kübitlere dönüştürmesine olanak sağladı. 10 kübitlik sihirli durumlar, yalnızca sabit faktörlü bir ek yük kaybıyla standart tek kübitli ve üç kübitlik sihirli durumlara dönüştürüldü.
Bu iki yenilikle ekip, kübit sistemleri için sabit ek yükün (γ = 0) elde edilebileceğini kanıtladı.
Önemi ve gelecekteki çalışmalar
Sonuç, temel bir teorik sınır oluşturur: sihirli durum damıtma ek yükü için daha iyi bir asimptotik ölçeklendirme mümkün değildir. Ancak Wills, teori ile kısa vadeli uygulama arasındaki boşluğu vurguladı.
Buradaki zorluk gerçek kaynak gereksinimlerinde yatmaktadır. γ = 0 ölçeklendirmesi teorik olarak optimal olsa da, protokolün uygulanması, yakın vadeli kuantum bilgisayarların sağlayabileceğinden çok daha fazla fiziksel kübit gerektirebilir.
Bununla birlikte, teorik temellerin oluşturulması, hataya dayanıklı kuantum hesaplamanın geliştirilmesi için hayati önem taşımaya devam ediyor.
“Sağlam bir kuantum büyüsü teorisi geliştirmek, tüm rejimlerde hata toleransını daha da ileri taşımak için inanılmaz derecede önemlidir, çünkü bunun evrensel kuantum hesaplama için gerekli olduğunu biliyoruz” dedi. “Bunun gibi çok teorik bir çalışmayı, fikirleri yakın vadeye uyarlamayı amaçlayan daha pratik odaklı çalışmaların takip etmesi oldukça yaygındır.”
Ekip, Wills’in enine adreslenebilir kapılar üzerindeki son çalışması da dahil olmak üzere uzantıları keşfetmeye başladı. Gelecekteki talimatlar arasında sabit faktörlerin optimize edilmesi, kuantum LDPC kod değişkenlerinin araştırılması ve optimal kudit-kubit dönüşümlerinin belirlenmesi yer alıyor.
Yazarımız Tejasri Gururaj tarafından sizin için yazılan, Stephanie Baum tarafından düzenlenen ve Robert Egan tarafından doğrulukları kontrol edilen ve gözden geçirilen bu makale, insanların dikkatli çalışmasının sonucudur. Bağımsız bilim gazeteciliğini canlı tutmak için sizin gibi okuyuculara güveniyoruz. Bu raporlama sizin için önemliyse lütfen bağış yapmayı düşünün (özellikle aylık). Bir alacaksın reklamsız bir teşekkür olarak hesaplayın.