Delft’teki Qutech’teki araştırmacılar, kararlı kuantum hesaplamasını mümkün kılabilecek özelliklere sahip majorana bağlı durumları gözlemlemek ve manipüle etmek için süperiletkenleri ve kuantum noktaları birleştirdiler. İki boyutlu bir elektron gazında üç birleştirilmiş kuantum nokta zinciri oluşturarak, majorana bazlı kuantum bitlerinin incelenmesi için gerekli olan Majoranas’ın özelliklerini gösterebildiler.
Sonuçlar şurada yayınlandı Doğa.
Kuantum hesaplamadaki temel sorunlardan biri, kuantum bitlerinin doğal istikrarsızlığı olmaya devam etmektedir. Hataya toleranslı kuantum bilgisayar arayışında, topolojik kuantum bitlerinin hatalara önemli ölçüde daha az eğilimli olması beklenmektedir. Bu kubitlerin anahtarı, tek boyutlu süper iletken sistemlerin zıt kenarlarında görünmesi tahmin edilen majorana bağlı durumlar olarak adlandırılan quasipartiküllerdir.
Kıdemli yazar Srijit Goswami, “Yıllarca, Majorana Bağlı Devletler için yapılan bu arama, genişletilmiş tek boyutlu yarı iletken-süper-iletken hibrid cihazlara odaklandı. Bu sistemler, bu sistemlerin, majör sınırlı devletleri güvenilir bir şekilde incelemeyi ve maddi kalite majörünü güvenilir bir şekilde incelemeyi çok zorlaştıran bozukluktan muzdarip hale getirdi.”
Üç yapay atomlu Kitaev zincirleri
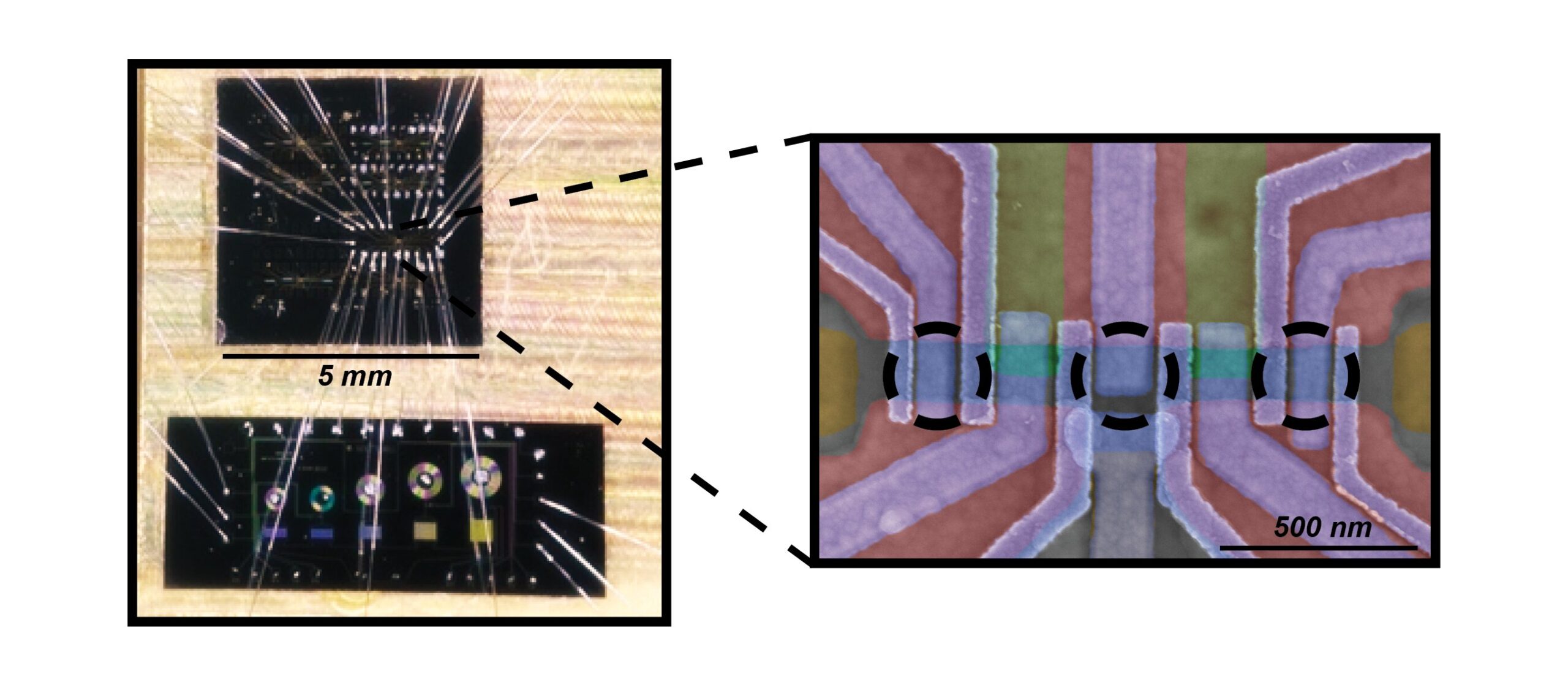
Yüksek kontrollü bir model sistemi oluşturmak için Delft ekibi, 2000 yılında Majoranas’ı tahmin eden temel Kitaev modeline geri döndü. Kuantum noktaları (QDS) adı verilen yapay atomlar zincirinde bir “blok-blok” sistemi oluşturdular. Bu teknik, majorana bağlı devletleri sistematik ve deterministik bir şekilde mühendislik yapmalarına izin verdi.
Geçtiğimiz yıllarda, farklı malzeme platformlarında çalışan teorisyenlerin ve deneysel ekiplerin güçlü bir kombine çabasıyla, Qutech’teki araştırmalar bu kitaev zincirlerinin anlayışını önemli ölçüde ilerletti. Nanotellerde ve iki boyutlu elektron gazlarında (2deg) iki bölgeli zincirlerin incelenmesinden başlayarak, şimdi bu zincirleri uzatmak ve Majoranas’ın özelliklerinin nasıl geliştiğini anlamak mümkün hale geldi.
Nanotellerde üç bölgeli zincirler üzerinde yapılan son çalışmaları tamamlayan bu çalışma, 2deg’lerin majoranas’ı sistematik olarak oluşturmak, manipüle etmek ve araştırmak için nasıl kullanılabileceğini gösterir.
İlk yazar Bas Ten Haaf, “Kuantum noktalarının etkileşme şeklini dikkatlice ayarlayarak, Majoranas’ın aynı anda sistemin solda ve sağ tarafında, ortada değil, ortaya çıktığını açıkça gözlemledik.”

Topolojik kubitlerin istikrarı, iki majorana bağlı devleti fiziksel olarak ayıran ve onları birbirlerini “imha etmekten” uzaklaştıran bir “yığın boşluğunun” varlığına dayanır. Delft ekibinin model sisteminde, orta kuantum nokta seçici olarak mevcut veya çıkarılabilen ayarlanabilir bir dökme boşluğu görevi görür.
Ten Haaf, “Bu boşluğu çıkardığımızda, dış kuantum noktalarındaki majorana bağlı durumlar, tam olarak Kitaev’in tahmin ettiği gibi artık kararlı değil” diyor. “Kitaev modeli çok basitleştirildi. Bu bir oyuncak modeli. Gözlemlerimizin onunla ne kadar iyi anlaştığını görünce şaşırdım.”
Majorana’ya bağlı durumların imzaları daha önce bildirilmiş olsa da, bu, sol, orta ve sağ tarafta olanları aynı anda araştırmak için minimal bir model sistemi kullanan ilk çalışmadır.
Majoranas’ı hareket ettirmek
Yazarlar ayrıca Majoranas’ın yerinin bir QD’den diğerine taşınabileceğini göstermek için sistem üzerindeki kontrollerini kullandılar. Majoranas’ı hareket ettirme yeteneği topolojik kuantum hesaplama için önemlidir. Bu uzun süredir aranan teknolojide, Majoranas’ın pozisyonları, bilgiyi rastgele hatalara karşı sağlam bir şekilde kodlayan karmaşık örgü kalıpları oluşturmak için değiştirilir.
Delft ekibi, iki majörün pozisyonlarını gerçekten değiştirebilmeleri için daha fazla kuantum nokta eklemeyi planlıyor. Goswami, “Altı kuantum noktadan yapılmış bir T şekli, örgülü operasyonları test etmemize ve temel bir kubit oluşturmamıza izin verecek.” Diyerek şöyle devam etti: “Bu en iyi kubit olmayacak, ancak Majoranas’ın temel özelliklerinin çalışmalarına izin verecek.”
Goswami, “Kuantum noktalarımızla bir kuantum bilgisayar inşa etmekten çok daha fazla büyüleyen şey, bu majoranaların nasıl çalıştığını ve onlarla neler yapabileceğimizi ortaya çıkarmak. Nasıl etkileşimler? Nasıl çiftler? Bunlar keşfetmeye çalıştığımız şeyler.”