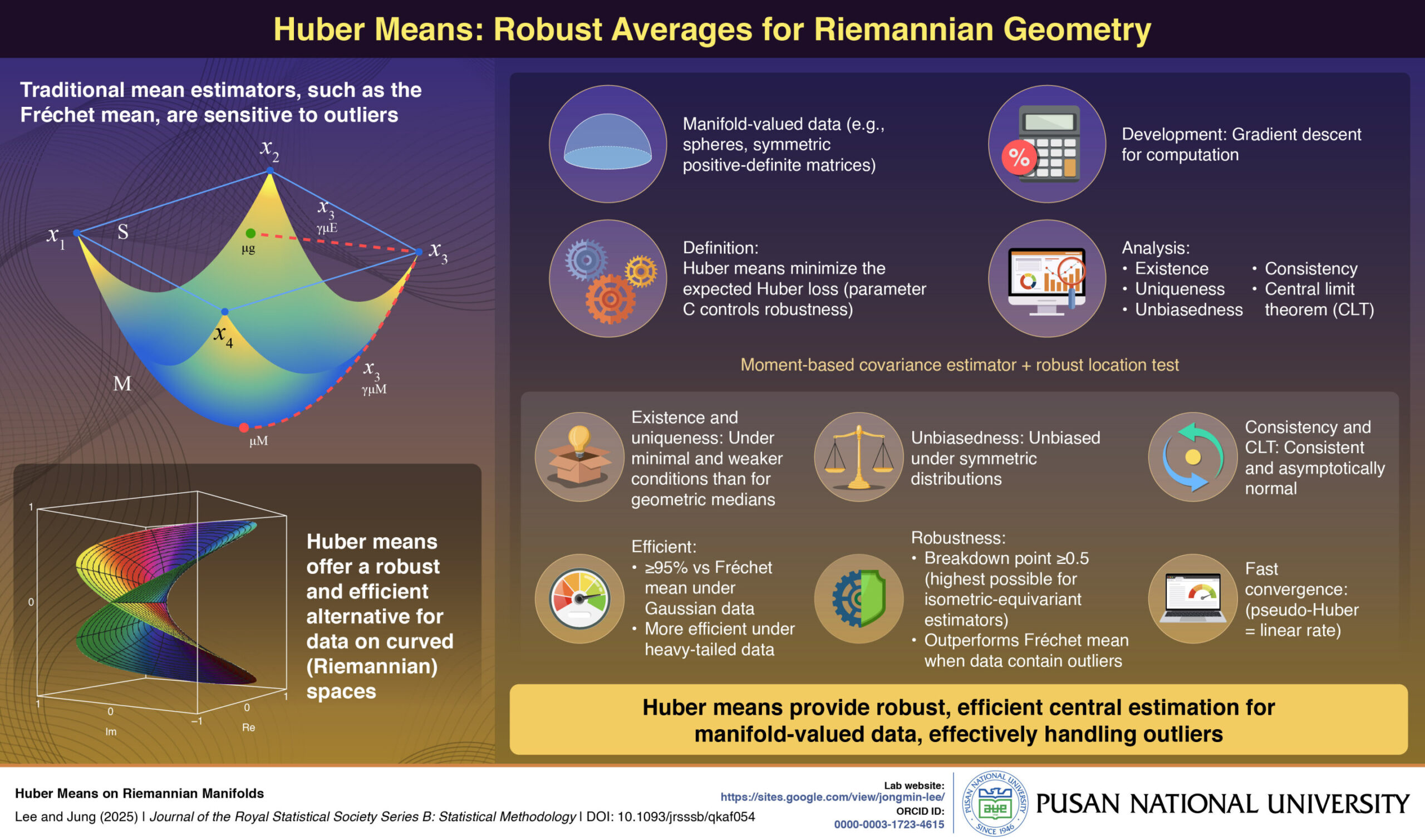
Karmaşık verilerin yönlendirdiği bir çağda, bilim insanları giderek daha fazla gerçek olmayan bilgilerle karşılaşıyor.’Düz Öklid yüzeylerinde düzgün bir şekilde durmazlar. 3 boyutlu tıbbi taramalardan robot yönlendirmelerine ve yapay zeka dönüşümlerine kadar günümüzde çoğu şey’Veriler, Riemann manifoldları adı verilen kavisli geometrik uzaylarda yaşar. Bu tür verileri doğru bir şekilde analiz etmek, özellikle gürültü veya aykırı değerlerin sonuçları bozduğu durumlarda hala bir zorluk olmaya devam ediyor.
Bu sorunu çözmek için Pusan Ulusal Üniversitesi İstatistik Bölümü’nden Profesör Jongmin Lee, Seul Ulusal Üniversitesi’nden Profesör Sungkyu Jung ile işbirliği içinde, kavisli uzaylarda veri analizini daha sağlam ve güvenilir hale getirmek için tasarlanan Huber ortalaması adı verilen yeni bir istatistiksel yöntem geliştirdi. Çalışmada yayınlandı Kraliyet İstatistik Derneği Dergisi Seri B: İstatistiksel Metodoloji 25 Ağustos 2025’te, Huber kayıp fonksiyonunu entegre ederek, verimliliği ve aykırı değerlere karşı direnci tek bir zarif çerçevede birleştirerek klasik Fréchet ortalamasının sağlam bir genellemesini sunuyor.
Lee, “Çalışmamız, Riemann manifoldları üzerindeki klasik Fréchet ortalamasının sağlam bir genellemesini ortaya koyuyor” dedi. “Bu, aykırı değerlere karşı daha fazla istikrar sağlar ve geometrik veriler üzerindeki istatistiksel analizin güvenilirliğini artırır.”
Huber ortalaması, tipik gözlemler için L₂ (en küçük kareler) kaybını ve büyük sapmalar için L₁ (mutlak sapma) kaybını kullanarak veri yapısına otomatik olarak uyum sağlar. Bu denge, 0,5’lik bir arıza noktasına ulaşmasını sağlar; bu, verilerin yarısı aykırı değerler veya aşırı değerler olsa bile tahmincinin güvenilir kalması anlamına gelir. Çalışma aynı zamanda pratikte hızla yakınsayan yeni bir hesaplama algoritmasının yanı sıra tahmincinin varlığı, benzersizliği, yakınsaması ve tarafsızlığı için teorik garantiler sağlıyor.
Lee, “Bu yöntem, bilgisayarla görme, tıbbi görüntüleme ve şekil analizi gibi alanlarda potansiyel uygulamalara sahip olan Öklid dışı ortamlarda daha sağlam veri analizine olanak tanıyor” diye açıkladı.
Bu uygulamalar bilimsel ve mühendislik alanlarına yayılmaktadır. Tıbbi görüntülemede Huber ortalaması, beyin veya organ şekli verilerinin ortalamasını iyileştirerek daha doğru teşhislere yol açabilir. Robotikte, gürültülü veya öngörülemeyen ortamlarda bile sistemlerin hareket ve yön verilerini daha iyi yorumlamasına yardımcı olabilir. Yapay zeka ve makine öğreniminde geometrik veriler (bağlantılı rotasyonlar, grafikler veya dönüşümler) üzerinde çalışan modelleri daha dayanıklı ve daha adil hale getirebilir.
Lee şunu ekledi: “Sağlam ve geometrik olarak bilinçli veri analizi için bir temel sağlayarak bu araştırma, gerçek dünyayla etkileşime giren yeni nesil güvenilir yapay zeka, hassas tıp ve akıllı teknolojileri sessizce destekleyebilir.”